The Proceedings of the 1989 NanoCon Northwest regional nanotechnology conference, with K. Eric Drexler as Guest of Honor.

Return to NanoCon Top
Return to NanoCon Proceedings Table of Contents
Return to Jim's Molecular Nanotechology Home Page

NANOCON PROCEEDINGS page 2


III. MOLECULAR MANIPULATION and MOLECULAR COMPUTATION

Introduction by Jim Lewis

Last night Eric talked about a number of paths leading towards advanced molecular technology. Two paths that were mentioned were protein engineering and the scanning tunneling microscope. Today we will be talking about aspects of molecular technology that have nothing to do with either of these approaches, although one of the subjects was published in a journal called protein engineering. First Eric will discuss devices that could be built if we had assemblers and will elaborate on the mechanical nanocomputers that he briefly mentioned last night. Afterwards, Ned Seeman and Bruce Robinson will talk about using DNA to build small computers of a very different sort. Their approach is particularly novel in using DNA for its structural properties, instead of as the informational molecule that molecular biologists have studied. Ned will first discuss some experiments to design DNA that can self-assemble into various types of molecular structures. Bruce will then discuss work with synthetic polymers to hang functionality unto these structures. I will challenge the audience to be aware during these presentations that we will hear two very different visions for basically the same sort of thing - a molecular computer. This diversity of approaches illustrates a point that Eric made last night. One of the things that gives us confidence that nanotechnology is a real possibility is the multiplicity of pathways that are leading us in that direction.

A. Eric Drexler: Rod Logic for Molecular Computing

Yesterday I set a context for discussing complex systems built to atomic specifications and discussed my goal as exploratory engineering. An exploratory engineer attempts not to build sound artifacts, but to build sound arguments for a class of artifacts. This is very different from what we will hear about later this morning, which is attempting to make things that actually work that can be done with technology that is relatively accessible.

Yesterday I discussed how working with polymers that fold up into objects gives us one toe-hold in the domain of molecular engineering. I expressed how self-assembly could lead to the construction of complex molecular mechanisms, how that opened a path to assemblers able to build complex structures by positioning reactive molecules, and how advanced assemblers will resemble industrial robots, being programmable devices able to do very general positioning of tools to accomplish engineering purposes.

That vision of assemblers pre-supposes the ability to execute complex programmable motions in a reliable way on a molecular scale. If one can make a case for mechanical nanocomputers, one will have a case for complex programmable motions because the computers themselves are based on moving parts.

I mentioned the notion of molecular electronics and noted that it is probably the preferred way to go, but to do design and analysis of those systems one has to look at quantum phenomena because electrons are very light particles and have wave functions that are very spread out on a nanometer scale. People are doing excellent work in this direction, but it is not something that I can build on.

I have been looking at cruder devices analogous to the Babbage engine, but building more directly on the methodologies that have been developed for integrated circuits; i.e., using binary instead of base-10 logic.

The basic advantage is that you can use classical mechanics as a good enough approximation for most purposes in analyzing the behavior of these systems. Nuclei are massive and are thus well localized. The Born-Oppenheimer approximation says that you can separate out the quantum mechanics of electrons from the quantum mechanics of nuclei. It turns out that you can then throw out the quantum mechanical description of the nuclei and describe them simply as masses that have an energy as a function of their position with respect to other masses. Thus you can get forces, vibrations and such that you can describe in classical physical ways.

Chemists occasionally worry about tunneling; they do that almost exclusively when thinking about the lightest nuclei, protons, the nuclei of hydrogen atoms. Even then it is only a minor correction, primarily at low temperatures. At ordinary temperatures, it's not the quantum mechanical uncertainty that is responsible for the bulk of the engineering uncertainty, but instead the main source of uncertainty is thermal noise.

The systems that result from this design approach are compact. They are likely to be competitive with molecular electronics in compactness. They can also approach the theoretical limits of efficiency of computation in energy utilization. But they are somewhat slow - a little faster than present day computers, but a lot slower than what one would expect from molecular electronics.

1. Constraints on Molecular Design

A number of restraints come to the attention of molecular engineers in designing such systems.

2. Molecular Mechanics

Molecular mechanics treats covalent bonds between atoms as being like springs, with characteristic lengths, tensile strengths and spring constants. In a linear approximation you find that pulling two carbon atoms apart results in a restoring force of 220 Newtons/meter. That approximation breaks down if you stretch them distances comparable to the bond length, which is ~ 0.15 nm.

There are a number of molecular mechanics force fields that deal with more complicated energy terms as well. Covalent bonds also have preferred directions with respect to one another. For carbon atoms, a preferred geometry is to have four bonds coming out in a tetrahedral arrangement. Changing bond angles also results in a spring-like restoring force. These forces are, however, weaker than the ones affecting bond length.

I would like to encourage people to use their physical intuitions because we are already familiar with the kinds of forces that we are talking about here. If you were to take a hunk of this podium and whittle it down until you got to something of molecular size, you would find that you had something with size, shape, mass distribution, stiffness, etc. Molecules can be thought of as the smallest instances of ordinary physical objects.

From an exploratory engineering perspective, this has a nice property. If you have an abstract design that clearly works if its large enough, and if you go through a design exercise that says that you think that you can make something this small with the atoms arranged in a particular way, then if you should happen to be wrong, it is likely that if you scale it up a little bit to make it more like the systems with which we are familiar, that you would have a working system. Thus failures in design can be relatively soft failures, although one tries to allow enough safety margin in the design to prevent failures.

3. Transmitting Signals in a Nanocomputer

To run a computer, you need a way to transmit signals inside. In a conventional microcomputer, to transmit a signal you put a voltage on a wire (a conducting path on silicon). In a nanocomputer, an analogous thing to try is to put a displacement on a rod.

This rod [Editor's Note: The slide showed a carbyne structure, a chain of carbon atoms connected by alternating single and triple bonds] has several virtues. (i) It's only one atomic diameter so that it's a very slim rod. (ii) All of the bonds are in a straight line. (iii) The bonds are all very strong, stiff covalent bonds. The fact that they are in a straight line means that you can not make the rod longer by bending a bond. That increases stiffness.

This rod is very smooth. For one rod to sense that another rod had undergone a displacement, we have to have some additional structure. One possible structure that meets the requirement for such a knob is this. [Editor's Note: The slide showed a couple of fused three-ring heterocyclic structures with a few strategically placed protruding fluorine atoms.] Just looking at these, you might say that this could be synthesized by organic chemistry, and then you might look at it a bit closer and decide that you couldn't. That's fine; the proposition is not to synthesize these by bulk chemistry.

Rods with "gate" and "probe" knobs can be used to build a logic element such that one rod will move if and only if the knob on the other rod has been pulled out of the way. So the motion of one rod is contingent on the position of another. That's directly analogous to a transistor, in which the ability of current to flow in one conducting path is dependent on the voltage of another conducting path. Thus you can build mechanical nanocomputers with the same logic systems used in conventional electronic computers.

For this to work, the moving parts must be embedded in a matrix with tightly fitting, intersecting channels to make sure the rods stay in place and can be blocked. That matrix contains far more atoms than the moving parts. It is a far more formidable challenge, both to synthesize and to design, than are the moving parts. The matrix will involve several hundred atoms per logic gate.

[Editor's Note: Eric used cross-section pictures of his proposed rod logic system, showing the channels in the matrix and the rods with gate and probe knobs, to illustrate how the assembly would be mobile in one set of starting positions and immobile in another. Details of this and other aspects discussed in this talk can be seen in Eric's paper "Rod logic and thermal noise in the mechanical nanocomputer" K Eric Drexler. Proceedings of the Third International Symposium on Molecular Electronics Devices, Elsevier Science Publishers B.V. (North Holland), in press. A reprint can be obtained from the Foresight Institute, see below.] [Editor's 1996 Note: These and related topics are treated in detail in K. Eric Drexler's 1992 technical book Nanosystems..]



Above: Mechanism for two nanocomputer gates, initial position. One control rod with two gate knobs is seen laterally; two more rods with knobs are seen end on. Each rod with associated knobs is a single molecule.
Below: The lateral rod has been pulled to the left during computation. Notice that one of the end-on rods has now been blocked and the other one unblocked in mechanical mimicry of the transistor action.




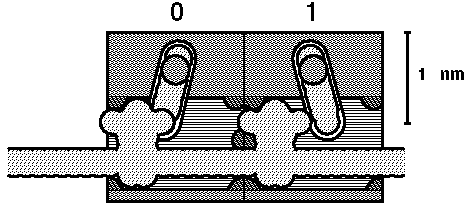
It turns out that the ability to have one rod motion switch some things on and other things off at the same time makes this more analogous to CMOS technology than to NMOS technology. There are thus parallels not just to microelectronics but to particular styles of microelectronics.

4. Computing with Sliding Rods

An additional complexity appears when you look at how to use sliding rods to do computation. Once you've moved a rod in a computation cycle, you have to move it back again. That's different from microelectronics in which you don't have to take the electrons and put them back where they came from, although you do have to cycle voltages back.

I'll describe how this is a NAND gate. A NAND gate is something that has a "1" output if and only if both of the inputs are "0." [Editor's Note: Eric used a diagram to illustrate that one rod can move as long as another has not moved across.] As long as one rod is in a "0" state, the output rod will continue in a "1" state.

To reset the rod after it has moved, we have a spring at one end. Another spring is needed to give a compliant element in the system so that something can stretch if a rod is pulled on that can't move because its blocked.

Finally, if you have a number of output paths, you need some way of aligning these knobs so that this segment rod is well-aligned (this is a thermal noise consideration). We have a seating knob that provides a mechanical reference point for the rod, and when its pulled it provides a reference point to anchor the rod in the other position.

5. Thermal Noise

I mentioned thermal noise considerations and tied those to mechanical stiffness. If a mechanical system is very stiff, then a small displacement costs a lot of energy. Conversely, if a system is very compliant, then a small energy fluctuation causes a large displacement. The probability of getting a particular amount of energy in a vibrational mode is an inverse exponential function of the amount of energy specified. To have a low error rate (a low probability of something being far enough out of place to cause a problem) you need to have a system that is sufficiently stiff that the energy required to cause a problem is improbable. In a paper that I did entitled "Rod Logic and Thermal Noise in the Mechanical Nanocomputer", which will appear in the Third International Symposium on Molecular Electronic Devices, I discussed the statistical mechanics of long flexible rods in constrained channels. You can calculate a probability distribution for the amount of rod shortening due to lateral fluctuations (wiggling). [Editor's 1996 Note: These and related topics are treated in detail in K. Eric Drexler's 1992 technical book Nanosystems..]

Rods can also stretch. This can be calculated, although it has complications. The longer the rod, the higher the error rate. For one error per 1012 gate operations, the output segment is limited to being 16 gates long.

6. Programmable Logic Arrays

Why would you want a lot of inputs and outputs on one rod? A class of structure widely used in designing integrated circuits is a programmable logic array. In Mead and Conway's book INTRODUCTION TO VLSI SYSTEMS, there is a description of an NMOS circuit based on a programmable logic array. Re-implementing it in rod logic gives you about a factor of a hundred in increased speed. The way that this system works mechanically is that you have a bundle of rods that is yanked, and they are mobile or immobile depending on the status of registers. This set of vertical rods thus moves or doesn't move and thus blocks or unblocks this horizontal set of rods. Yanking the horizontal rods in turn blocks or unblocks the set of vertical rods so that at the next stage of the computation you yank the vertical bundle, etc. The pattern of information is then stored in some registers. The bundle of rods can then be un-yanked to reset them, as can the other bundle so that the mechanism can be re-used.

7. Thermodynamic Reversibility

Each of the steps of pulling a rod up against another and then releasing it is a mechanically reversible operation. As each spring is stretched and un-stretched, work is done and then recovered. Assuming that the motions are slow and smooth, the whole process is thermodynamically reversible. Charles Bennett and Ed Fredkin (of MIT) along with Rolf Landauer have described the thermodynamics of computation and they conclude that this kind of combinatorial logic can in principle be thermodynamically reversible. In the limit of slow motion, this system matches that ideal. The main loss results from one knob losing vibrational freedom as it is pushed against another knob.

That is like compressing a gas molecule in a cylinder. If you do it slowly enough, the process is isothermal and reversible because the temperature of the gas is the same after it has expanded as before it was compressed and the force applied on the way in is the same as what you get back on the way out. If instead the compression is done fast, the gas heats as it is compressed and then cools as it expands. In this case you get less work out as it expands then you put in to compress the gas so that you have a thermodynamic irreversibility. At finite clock-rates, that compression loss (due to non-isothermal operation) is the main source of energy dissipation in these devices that I have identified so far. This is one of the fuzzier numbers in this analysis because analyzing dynamic friction in these devices is not easy.

8. Data Registers

What happens in the registers? The other result from the gentlemen that I mentioned above concerning the thermodynamics of computation is that if you write a bit into a register and then erase it, that cycle must in principle expend ln2 [Editor's Note: natural logarithm of 2 = 0.6931...] times kT (where kT is a measure of the energy of a vibrational mode at a temperature T). It wastes that amount of free energy per cycle.

One can design a register that can store and erase data that approximates that limit. [Editor's Note: Eric showed a diagram of his design. The "this" references in the transcript will be a bit confusing without the diagrams, but reprints of the technical papers can be obtained by sending a donation to the Foresight Institute -- see below.] We start with a data rod that, at the end of one of the combinatorial logic cycles either moves or does not move. We want to record whether or not the rod moved so that it can be reset for another computational cycle. The register includes the data rod, another rod called a plunger, and a bit token. This token is a knob sticking out of a rod, and it is free to move around almost like a gas molecule. It can either block or not block a rod and thus store a "1" or a "0" that can be used in a molecular mechanical computation. If the data rod is in a "0" state (it doesn't move) the plunger is pushed over, confining the bit token to the left. The next step in the cycle is to move the latching surfaces together and hold this in place as the plunger is moved back, recording the fact that this has not moved. The other thing that can happen is that the data rod is in a "1" state (it can move) so it moves one way while the plunger moves the other and they meet in the middle. The one is a stiff structure, the other is mounted on a relatively soft spring so that when they meet, it continues to push and confines the bit token on the right. Moving the latching surfaces together records the fact that the rod moved as we reset the process for the next cycle of combinational logic.

If we were to reverse all of the above steps, this would be a reversible process, but in the course of doing so we would have to had recorded some place else what the result was. If we don' t know that result anymore, then the only way to erase the result is not to reverse the process that I have just showed, but to simply move the latching surfaces apart. Then the confined bit token is free to move, just like the free expansion of a gas into twice the volume. We thus lose the information about on which side the bit token was confined, and thus the entropy increases irreversibly.

9. Mechanics

This diagram shows the choreography of one and a half cycles of motion in a programmable logic array. Each step is shown as a ramp instep of a step because moving these things involves acceleration, motion, and deceleration. Looking at this with Newtonian mechanics, the mass of a rod is about 0.02 attograms (2 x 10-20 grams). The typical displacement of such a device is a healthy fraction of a nanometer. A good time interval (several times the acoustic transmission time so that these rods can be analyzed as more or less rigid bodies) is about 50 picoseconds (trillionths of a second). The peak speed is about 20 meters per second. In general, one finds when analyzing molecular mechanical motions that the speeds are in a familiar range - meters/sec - because this quantity depends on strength to weight ratio, not on size. On the other hand, acceleration of a rod is about 0.1 trillion G's. Such a huge acceleration would get you near the speed of light in less than a second if it could be maintained, which it can not because of the strength to weight ratio. The force required to produce this huge acceleration is only 24 piconewtons. Since the breaking strength of the rod is measured in nanonewtons, that is a modest stress. The peak kinetic energy of the rod is comparable to the energy of motion of a molecule of air in this room.

10. Computers from Molecular Mechanical Components

These computing devices are smaller than the transistors that were commonly in use in computers a couple of years ago by a factor of 104 in linear dimension, which means 1012 in volume. Thus a device of the capability of a single chip microprocessor, like the Z80 or Motorola 68000 made with 3 micron technology, could be put into a volume of 1/1000th of a cubic micron.

For random access memory, you should get nanosecond access times with 5 cubic nanometers per bit, or allowing for overhead, a density of about 1020 bits per cubic centimeter. That's more information in a cubic centimeter than people have written down since they started making marks on papyrus.

Tape memory gives you another factor of 100 in memory density. Bits would be stored by the presence of a bulky or less bulky side group on a polymer chain, such as polyethylene. To read the tape, you would mechanically probe it to find out how bulky the side group was. The write operation would involve chemical transformation. A reasonable length for such a tape is several microns; a reasonable spooling speed is like a meter per second. To get from one end of the tape to the other is thus a matter of microseconds. We're talking here about tape systems that are far faster than present day hard drives.

Estimates of power dissipation are relatively fuzzy. Making a gigahertz clock assumption and assuming a dissipation of 50kT per bit of a 32-bit word per cycle, we're talking of power dissipation in nanowatts. For a single device in good thermal contact with its environment that's a temperature rise of less than a thousandth of a degree Kelvin.

Thus a large computer can be small on the scale of a mammalian cell, giving some plausibility if you also assume some other hardware and a lot of software development, to the notion of cell repair systems. Also, yesterday I estimated the computational capacity that you could get in one cubic centimeter using this crude mechanical technology - more computational power in a desk top than exists in the world today.

There are a number of papers that discuss this and related topics. If you write to the Foresight Institute [Box 61058, Palo Alto, CA 94306] and send $5, you can get a packet of papers that describes these things in more technical detail. For a donation of $25, you can subscribe to the Foresight Institute newsletter "Foresight Update."

[For more up-to-date information, see the Foresight Institute home page. See also Chapter 12 of Nanosystems.]

Questions and Answers

AUDIENCE: You haven't described the bonds involved in your springs and in the matrix.

E. DREXLER: With respect to the matrix, I will plead complexity and say "Ah, that means there are lots of possibilities and one will probably work." The number of atoms per gate is in the hundreds, and the sorts of structures that one looks at are diamond-like. The channels would be atomically tailored surfaces to constrain the motion of the rods. It may turn out to be difficult to design a channel that properly grabs the type of rod that I've shown here so that it might be necessary to design a slightly bulkier rod. I'm going to be doing some more design work on that this year.
As for springs, the problem is typically making structures stiff, not springy. There seem to be a lot of choices in molecules to be springs, but I haven't done the design work to choose one yet.

AUDIENCE: With regard to the comparison you made last night between synapses and computers in which you modeled a synapse as a single gate that did something every millisecond, I read something suggesting that a synapse is more complicated and should be modeled more like an Apple II microcomputer.

E. DREXLER: If you want to model learning over time, it is clear that a synapse is considerably more than just a gate. It has to remember its history and modify its future operational parameters. In this sense, the comparison would favor the complexity of the brain compared to the computer that I was describing. On the other hand, if you look at the actual rate of operations that is possible in the brain within heat dissipation limits, Ralph Merkle at Xerox PARC has calculated that the brain can not (by a large factor) sustain a rate of one bit of computation per synapse per millisecond. I will simply say that those are fuzzy numbers, on balance the comparison seems reasonable, and there are no specific technical conclusions that follow from that comparison anyway.

AUDIENCE: In neural nets, connectivity is the major issue. Can you say anything about possible scaling up to form neural network architectures?

E. DREXLER: I have not looked at that. I've taken existing computer architectures and translated them into nano-mechanical systems. If superior architectures are available when this technology is ready for implementation, I assume that ways will be found. There are ways to get higher fan-outs using branching rods or an assembly of parallel rods.


Next page of the NanoCon Proceedings
Previous page of the NanoCon Proceedings
Return to NanoCon Proceedings Table of Contents
Return to Jim's Molecular Nanotechology Home Page
Return to Web Site Design and Authoring Services

Comments and correspondence? Send email to Jim Lewis:
nanojbl@halcyon.com
NanoCon Proceedings © Copyright 1989, by NANOCON
This page is part of Jim's Molecular Nanotechnology Web, copyright ©1996 James B. Lewis Enterprises. All rights reserved.
Last updated 24June96.
The URL of this document is: http://www.halcyon.com/nanojbl/NanoConProc/nanocon2.html